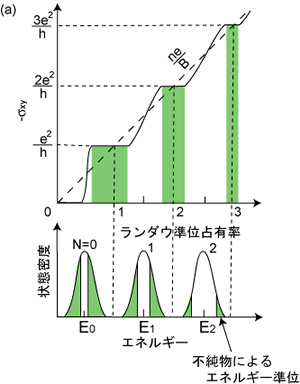
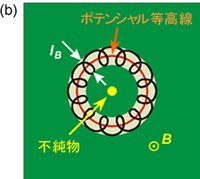
量子ホール効果 2次元電子系が強磁場下におかれて少数のランダウ準位しか占有しなくなったとき,ホール抵抗が磁場や電子密度に依存しない領域(プラトー)が現れ,その値がnを整数としてRH = h/ne2と量子化される現象を量子ホール効果といいます。特にnが整数値しかとらないので,これを整数量子ホール効果と呼びます。この量子化されたホール抵抗値は10-8という驚くべき高精度で一定なので,現在ではこれから決まるh/e2 = 25,812.806 Ωを標準抵抗として用いることになっています。また,不純物が少ないクリーンな系で電子密度を小さくするなどして電子相関を強くすると,nは整数に限らずある規則性をもった分数値もとることが分かっており,これを分数量子ホール効果といいます。これらの現象はともにノーベル物理学賞受賞の対象となりました。 なぜホール抵抗が量子化されるかを整数量子ホール効果を例にとって以下に簡単に説明します。「ランダウ量子化」のところで説明したように,2次元の空間に閉じ込められた自由電子に磁場を印加したとき,状態密度はEn = h/(2π)ωc(n+1/2) のエネルギーでδ関数的なピークをもちます。ホール伝導度はσxy=nee/B(neは電子密度)となり,電子密度や磁場を変化させてもプラトーは現れません。しかし,これは不純物のない理想的な場合であって,現実には(特に半導体では不可避的に)不純物効果によってランダウ準位はエネルギー幅をもちます。図(a)にあるように不純物準位中にフェルミエネルギーがきたとき,電子はローレンツ力をうけて不純物付近の等ポテンシャル面を磁気長lB(= √{h/(2πeB)})程度の幅をもって旋回するため(図(b)),伝導には寄与しなくなります。従って,不純物準位中でこのように電子が局在するエネルギー領域(図(a)の緑色の部分)では,ホール伝導度(及びホール抵抗)が一定,すなわちプラトーが生じることになります。電子密度もしくは磁場を変化させてフェルミエネルギーをランダウ準位のピーク付近に移動させると電子は再び伝導に寄与するようになり,伝導度は次のプラトーに向かって変化します。 分数量子ホール効果については,ここでは説明を省略しますが,「電子相関」が重要な役割を果たしており,多彩な量子相が実現していることが理論的に予測されています。
|
||||||